边打扑克边学插入排序算法（一）排序原理及代码实现

什么是算法、什么是时间复杂度、时间复杂度中的O标记是什么意思、如何分析算法的时间复杂度？咱们跟着兔小白和熊小猫，边打扑克边学！基础知识掌握好，后面学到复杂算法才会更从容！

熊小猫：晚上放松下，来我家打牌怎么样？

兔小白：不去了，我已经计划从今晚开始学习算法

熊小猫：在游戏中学习效果最好！其实抓牌的过程就存在一个算法！

兔小白：哦！？难道有抓到好牌的算法？

熊小猫：想什么呢！你说的是出老千！

兔小白：嘿嘿......

熊小猫：抓牌时候是不是要按顺序排放你手中的牌？这里就用到了插入排序。

兔小白：啊，之前我面试挂了，考的就是插入排序！没想到我打了20年扑克牌，竟然一直都在实践插入排序！？

熊小猫：今晚打完扑克，包你彻底掌握插入排序！

插入排序如何工作

下班后，兔小白来到了熊小猫家里打扑克。

兔小白：来吧！讲讲插入排序，请开始你的表演！

熊小猫：别着急，我先发牌。发完后，你再摸牌。边摸边思考下摸牌的过程。

兔小白：手里的牌需要从小到大排列，每次我摸牌后都会从小的一侧开始比较，直到找到比我抓到的牌大的那一张，然后插在那一张牌的前面

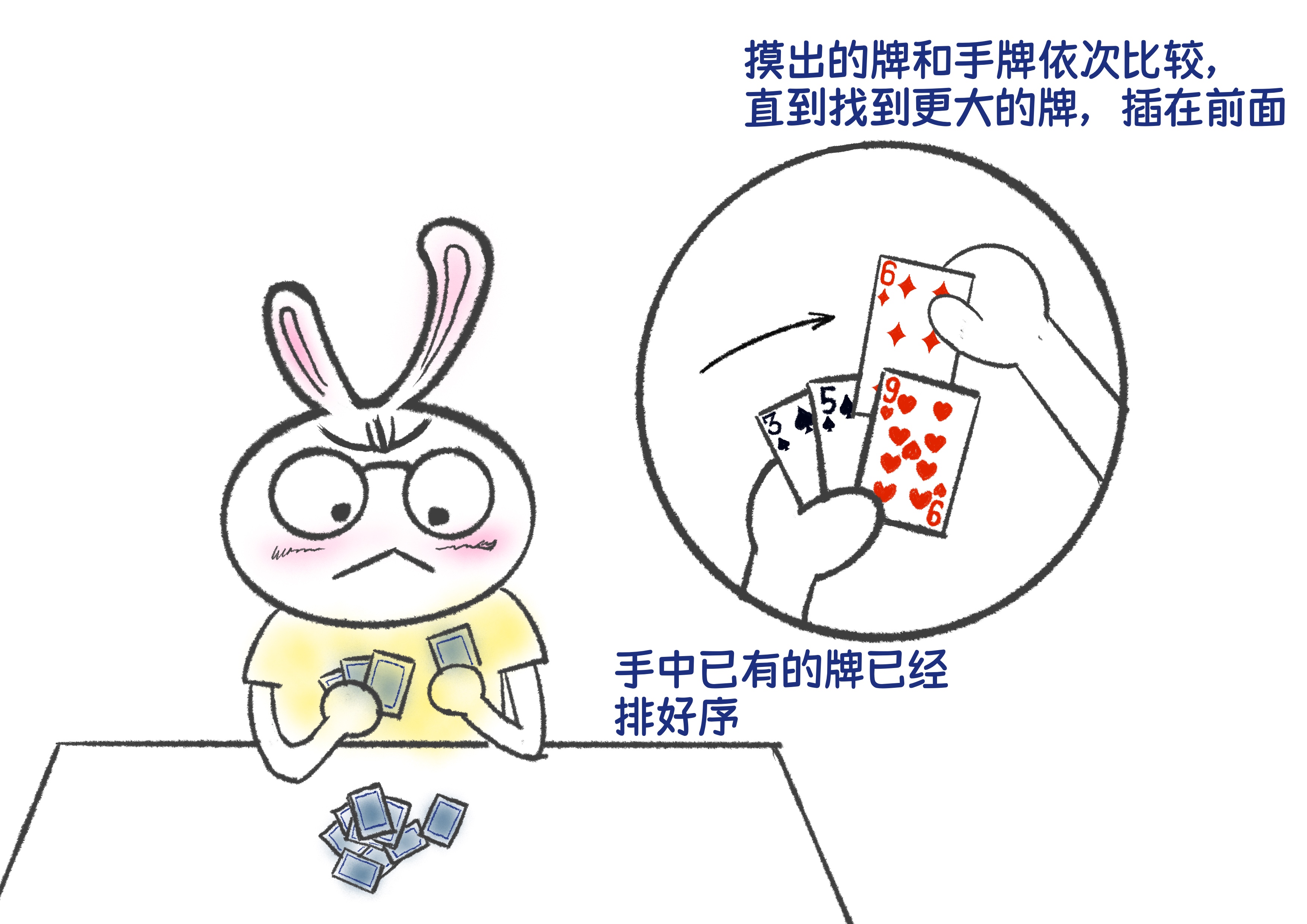
熊小猫：没错！这就是插入排序。我们仔细看看这个过程。

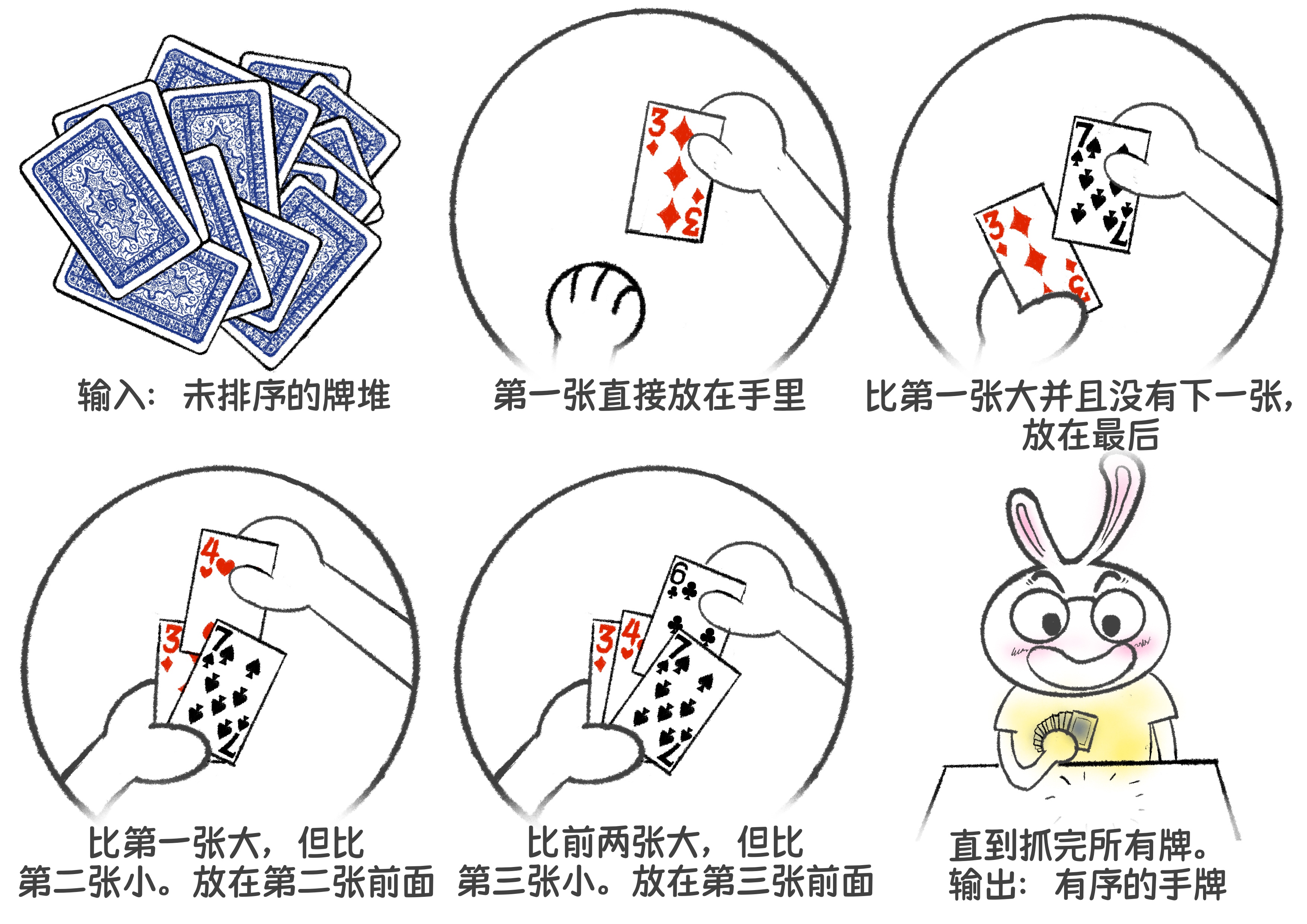
熊小猫：插入排序是不是很简单？你看看能不能用代码实现？

兔小白：等等！我的牌不错，先打完这局！

插入排序代码

熊小猫：你这牌也太好了，我认输了。

兔小白：作为惩罚，再给我讲讲代码实现吧？

熊小猫：没问题！咱先写一种最自然地，符合我们直觉地摸牌算法。首先你从牌堆里抓出一张牌，然后从左向右和手牌进行比较，找到比你抓到的牌大的那一张，你会把这张牌插入到它的前面。如果找到手牌的牌尾还没找到，那么放到牌尾。

兔小白：我想想......没错，确实我抓牌时候非常自然地就是这么做的! 但从你嘴里以这么严谨的逻辑说出来，我还得理解一下，嘿嘿！

熊小猫：那我们就按照这个逻辑写代码。

public static Integer[] sort(Integer[] unsorted) {
    //sorted数组可以理解为拿着排好序手牌的"手"
    Integer[] sorted = new Integer[unsorted.length];
    //第一张牌什么都不用想，放入手中
    sorted[0] = unsorted[0];
    //从第二张牌开始要逐张找到其顺序的位置放入
    for (int i = 1; i < unsorted.length; i++) {
        //摸起一张牌，从左侧开始比较，找到插入的位置。最差的情况要找到手牌的牌尾
        for (int j = 0; j <= i; j++) {
            //如果已经找到手牌牌尾或者中途找到手牌中比当前牌大的那张牌
            if (j==i || unsorted[i] < sorted[j]) {
                //比当前大的那张牌以及后面的牌向后移一位
                for (int k = i-1; k >= j; k--) {
                    sorted[k + 1] = sorted[k];
                }
                //将当前牌放入移动后空出来的那个位置。
                sorted[j] = unsorted[i];
                //本轮结束
                break;
            }
        }
    }
    return sorted;
}

兔小白：注释都有了！但我还是看不太懂。

熊小猫：其实很好理解，咱们跟着注释一行行的看。

1. 函数的输入是一个无序的整型数组 unsorted，可以理解为桌面牌堆
2. 第3行初始化的整型数组 sorted，可以理解为你的“手”，用来放排好序的牌。这里记住，手中牌是 sorted 中放的牌，桌面牌堆是 unsorted 中放的牌。
3. 第5行代码是你抓出第一张牌时，手里还是空的。所以直接放入你的手里，也就是 sorted 的0号位置。
4. 第7行开始进入主要的算法逻辑。从第二张牌开始，逐一找到自己的位置放进来。直到抓完所有的牌，也就是循环完 unsorted。
   1. 摸起一张牌 unsort[i]，然后从左向右，和手中牌比较大小。摸起的是第 i 张牌时，你手中有 i-1 张牌。但最差的情况要比较 i 次，因为如果很不幸，你拿到的牌比手里的 i-1 牌都大，要再比较一次以判断是否走到现有手牌的牌尾。（第9行代码）
5. 第 11 行代码，就是在比较摸起的牌和手里的牌，目的是找到比摸起的牌大的牌的位置 j。条件语句中的 j==i 表示找到手牌牌尾也没有找到比摸到的牌更大的牌。
6. 13-15 行这个循环体做的事情是，将 sorted 中 j 位置后面的牌往后移一位，空出 j 这个位置，用来放摸到的牌。
7. 17 行代码便是将抓的牌 放入手中正确的位置 sorted[j]
8. 19 行的 break 表示一轮插入逻辑结束，也就是第 9 行的 for 循环结束。此时已经将这次抓到的牌放入手牌中正确位置。

如此往复 4.1～4.5，直到所有 unsorted 中的元素都有序的放入 sorted。

兔小白：代码逻辑和我抓牌时脑子里想的一模一样！！我脑子只是转了一下，代码表达出来居然写了这么多？

熊小猫：哈哈，别看代码多，但计算机执行起来可比你脑子快的多！

兔小白：我突然想到有时候我会先把牌堆的牌全拿到手中再排顺序。这样排序会不会更快？

熊小猫：这个问题的本质是如何评价算法，解决问题的办法不止一种，如何评价哪种更好呢？通常我们使用算法复杂度来评价算法。

兔小白: 算法复杂度？说来听听？

熊小猫：别急，上面我给出的算法并不是最经典的插入排序。我再送你一份经典的插入排序代码，加量不加价！这个算法就是你说的把牌全部拿到手中再排序，这样就只需一个数组，节省了存储空间。 算法的主要逻辑是，从第二个元素开始，和前面的元素逐一比较，如果自己较小，就和前面的交换位置，然后再继续和前面的比较。直到找到前面比自己还小的那个元素，就停在当前的位置，然后开始下一轮循环。

代码如下，你先自己研究下，看明白后加上注释。

public static Integer[] sortV2(Integer[] unsorted) {
    for (int i = 1; i < unsorted.length; i++) {
        for (int j = i; j > 0 && unsorted[j] < unsorted[j - 1]; j--) {
            Integer toBeSortedNumber = unsorted[j];
            unsorted[j] = unsorted[j - 1];
            unsorted[j - 1] = toBeSortedNumber;
        }
    }
    return unsorted;
}

兔小白：考我是吧？就这几行代码，五分钟搞定！

五分钟后兔小白给代码加上了注释

public static Integer[] sortV2(Integer[] unsorted) {
    //从第二个元素开始，向后逐一执行排序逻辑
    for (int i = 1; i < unsorted.length; i++) {
        //从待排序元素的位置开始，向前逐一比较。比自己大就交换位置，比自己小停止循环。
        for (int j = i; j > 0 && unsorted[j] < unsorted[j - 1]; j--) {
            //如果前一个元素比当前元素大，那么交换两个元素的位置
            Integer toBeSortedNumber = unsorted[j];
            unsorted[j] = unsorted[j - 1];
            unsorted[j - 1] = toBeSortedNumber;
        }
    }
    return unsorted;
}

熊小猫：代码是不是简洁多了。插入排序的算法复杂度是O(n^2)。你应该还看不懂，一会咱们再聊聊算法复杂度。

总结

插入排序的过程和抓牌一样。每张牌和已排好序的手牌逐一比较，找到位置插入。

经典插入排序逻辑以此为基础进行优化，在原序列上完成排序，减少了存储空间的使用。